EOJ Monthly 2018.10

输入格式

第一行一个整数 $T$，表示有 $T$ ($1 \le T \le 333~333$) 组测试数据。

每组测试数据有四行。第一行一个整数 $n$ ($2 \le n \le 2 \cdot 10^5$)，表示树的节点个数。节点从 $1$ 到 $n$ 编号。

第二行 $n-1$ 个整数 $p_2, p_3, \ldots, p_n$ ($1 \le p_i \le i - 1$)，分别表示 $2,3,\ldots,n$ 的父亲节点的编号。由于节点 1 是根, 它没有父亲。

第三行是一个长度 $n-1$ 的字符串 $s_2s_3 \ldots s_n$，依次表示节点 $2,3,\ldots,n$ 到父亲节点的边上的字符。$s_i$ 是英文小写字母。

第四行是一个长度为 $n-1$ 的 01 字符串 $a_2a_3 \ldots a_n$，依次表示节点 $2,3,\ldots,n$ 是否是终态。 1 表示是, 0 表示不是。由于字符串的后缀不可能是空串，所以显然节点 1 不是终态。

另外，保证 $T$ 组测试数据中的 $n$ 的和不超过 $2 \cdot 10^6$，且不存在两个节点 $u$, $v$ 满足 $p_u = p_v$ 且 $s_u = s_v$。

本题数据量较大，请注意输入输出上的优化。

输出格式

对于每组测试数据，如果是合法的后缀 Trie，输出一行表示原字符串；如果不是，输出 Illegal。

2
11
1 1 1 2 2 4 6 6 6 7
taioenadnn
0111011111
16
1 1 1 2 3 4 5 6 7 8 9 10 11 12 15
abnnaaannnaaana
100001100001101

Illegal
banana

提示

下图对应样例 1 中的树。

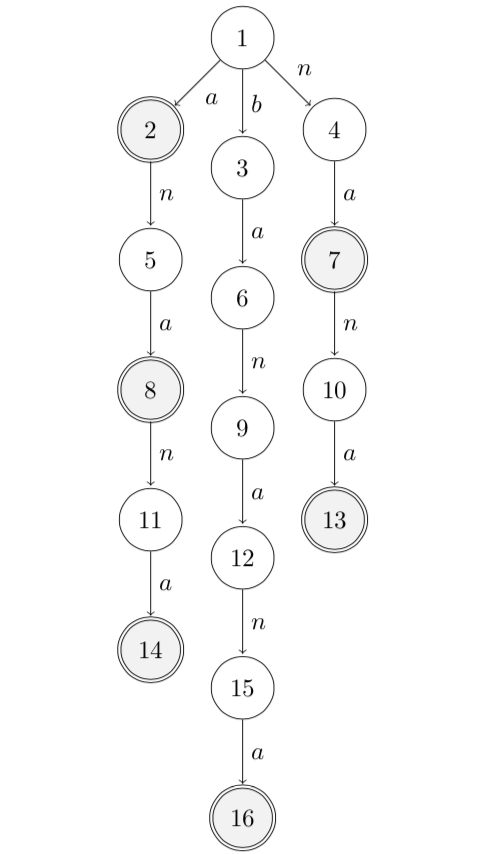
下图对应样例 2 中的树。