EOJ Monthly 2018.10
E. 盖房子
单点时限: 3.0 sec
内存限制: 1024 MB
给一个 $n \times m$ 的矩阵,每次询问一个等腰直角三角形内不同数字的个数。
输入格式
第一行两个数 $n$, $m$ ($1\leqslant n, m \leqslant 1000$)。
接下来 $n$ 行,每行 $m$ 个数表示矩阵,其中矩阵元素 $a_{ij}$ 满足 $1\leqslant a_{ij} \leqslant 100$。
接下来一个数 $q$ ($1\leqslant q \leqslant 5 \cdot 10 ^ 5$) 表示询问个数。
接下来 $q$ 行,每行三个数 $x,y,d$ ($1\leqslant x \leqslant n$, $1\leqslant y \leqslant m$, $d \geqslant 1$),分别表示等腰直角三角形的底的中点在第 $x$ 行第 $y$ 列,高是 $d$,保证这个三角形完全在矩形内。等腰三角形是底是竖着的,高是横着的,直角在底边的右边(见样例解释)。
数据保证,除了样例之外,矩阵元素都是在 $[1, 100]$ 内随机生成的。
I/O 量很大,请注意输入输出上的优化。
输出格式
对于每个询问,输出一个数,表示三角形内的不同数的个数。
样例
Input
4 3 1 1 1 2 1 2 2 2 2 2 2 2 3 4 3 1 2 1 2 3 1 2
Output
1 2 1
提示
样例中第三个询问的图示:
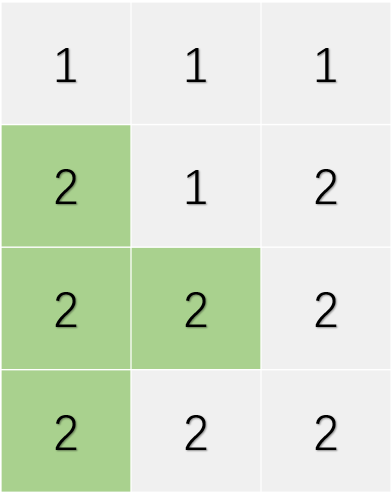
已结束
NaN
通知
比赛状态发生变化,点 OK 刷新。
通知