程序设计能力实训
单点时限: 2.0 sec
内存限制: 256 MB
When placing a board with a pinhole in the middle between an object and a screen, the reversed image of the object will appear on the screen. That is the so-called pinhole imaging.
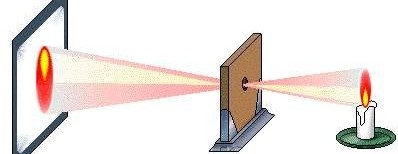
Assume that we have a candle and a screen. We know the distance $A$ between the pinhole and the candle. We also know the distance $B$ between the pinhole and the screen. We want to know the height of the fire displayed on the screen when we know the height $H$ of the real fire.
You could assume that the pinhole is very tiny and the screen is large enough.
输入格式
The input consists of multiple test cases. The first line of input contains an integer $T$, which is the number of test cases.
Each test case is on a separated line, and it consists three integers: $A, B, H$), separated by ONE whitespace.
$T$ is an integer, and $T \le 10$.
$A, B, H$ are integers, and $1 \le A, B, H \le 1~000~000$.
输出格式
For each test case, print a single line contains the height of the fire displayed on the screen, rounded to two fractional digits.
样例
2 1 1 1 2 1 2
1.00 1.00