程序设计能力实训
单点时限: 2.0 sec
内存限制: 256 MB
进制也就是进位制,是人们规定的一种进位方法。
对于任何一种进制–X 进制,就表示某一位置上的数运算时是逢 X 进一位。十进制是逢十进一,十六进制是逢十六进一,二进制就是逢二进一,以此类推,X 进制就是逢 X 进一。
现定义一种新的进制表示方法素数进制表示法。素数进制不是单一进制,在素数进制中,每一位的进制都各不相同,具体定义如下:
1、将素数从小到大排列成一个素数列表:$[2,3,5,7,11,13,17,19,23,29,31,\cdots]$。
2、在素数进制表示法中,从右边最低位开始,第 $n$ 位的进制定义为素数列表中第 $n$ 个素数,第 $n$ 位可用的数码为 $0$~(第 $n$ 个素数$-1$),第 $n$ 位对应的位权为素数列表中前 $n-1$ 个素数的乘积,第 $n$ 位上的数在运算时逢该素数进一位。即:右边最低位个位(第 $1$ 位)的进制为 $2$ 进制 (个位上可用的数码为 $0$,$1$),对应的位权为 $1$;十位(第 $2$ 位)的进制为 $3$ 进制(十位上可用的数码为 $0,1,2$),对应的位权为 $2$;百位的进制为 $5$ 进制(百位上可用的数码为 $0,1,2,3,4$),对应的位权为 $23$;千位的进制为 $7$ 进制(千位上可用的数码为 $0,1,2,3,4,5,6$),对应的位权为 $23*5$,依次类推。
例如:十进制整数 $2$ 的 素数进制 表示为 $10$ ($12+01$);
十进制整数 $6$ 的 素数进制 表示为 $100$ ($123+02+01$);
十进制整数 $38$ 的 素数进制 表示为 $1110$ ($1235+123+12+0*1$)。
给定一个非负十进制整数 $N$($N$ 的取值范围为 $[0,10^{18}]$),将其对应的素数进制的每一位按从高位到低位的顺序分别存放在一个单向链表中。
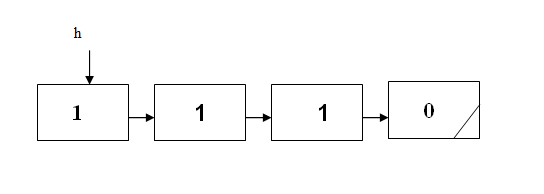
例如:$N=38$ 对应的素数进制值的单向链表表示为:
输入格式
第 1 行:整数 $T$ ($1 \le T \le 10$) 为问题数。
第 2∽T+1 行:每一个问题一行数据(数据的意义不在这里描述)。
输出格式
对于每个问题,输出一行问题的编号(0 开始编号,格式:case #0: 等),然后在一行中输出相关数据(数据的意义不在这里描述)。
样例
3 2 6 38
case #0: 1;0; case #1: 1;0;0; case #2: 1;1;1;0;
提示
可以考虑开一个结构体,保存素数进制的每一位,例如:
typedef struct Node
{ char value; //存贮素进制数的一位
struct Node *next;
}NODE;