1237. 链表运算 - 程序设计能力实训

单点时限: 2.0 sec

内存限制: 256 MB

运算符前置的算术表达式则称为波兰式。例如普通的表达式 2 + 3 的波兰式为：+ 2 3。波兰式的优点是运算符之间不必有优先级关系，也不必用括号改变运算次序。

例如：(2.5+3)(-4) 的波兰式为： + 2.5 3 -4，而 5-6*7 的波兰式为：- 5 * 6 7。

现给定一个用单向链表存贮的波兰式，其节点以字符串形式存放运算符和运算数。运算符包括+,-,*,/ 四种，运算数是浮点数，每个运算数的宽度不超过 10。测试数据保证除法运算的除数不等于 0。

要求定义函数 Evaluate 计算一个表达式的值。

例如：波兰式 * + 2.5 3 -4 的存贮为：

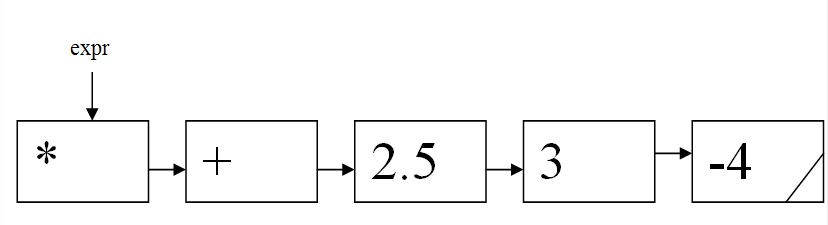
Evaluate 的返回值为-22。

结构体类型 NODE 表示一个单向链表的节点定义。

输入格式

第 1 行：整数 $T$ ($1 \le T \le 10$) 为问题数。

第 2∽T+1 行：每一个问题一行数据（数据的意义不在这里描述）。

输出格式

对于每个问题，输出一行问题的编号（0 开始编号，格式：case #0: 等），然后在一行中输出相关数据（数据的意义不在这里描述）。

样例

Input

3
3 2 +
-4 3 2.5 + *
7 6 * 5 -

Output

case #0:
5.00
case #1:
-22.00
case #2:
-37.00

提示

stdlib.h 中的函数 atof 把一个字符串转换成一个浮点数。

// ********** Specification of the structure **********
typedef struct Node { char value[100]; struct Node *next; }NODE;
/*/////////////////////////////////////////////////////*/
double Evaluate(NODE *expr)
/* PreCondition:
expr is the head pointer of a linked-list, which represents a
Poland expression
PostCondition:
return value of the expression
*/
{ //TODO: your definition
}
/*/////////////////////////////////////////////////////*/
/***************************************************************/
/*                                                             */
/*  DON'T MODIFY following code anyway!                        */
/*                                                             */
/***************************************************************/
#include <stdio.h>
#include <stdlib.h>
NODE *input()
{ NODE *h=0,*p;
do { p=(NODE*)malloc(sizeof(NODE)); scanf("%s",p->value); p->next=h; h=p; }
while (getchar()!='\n');
return h;
}
int main()
{  int i,t; scanf("%d\n",&t);
for (i=0;i<t;i++) printf("case #%d:\n%.2f\n",i,Evaluate(input()));
return 0;
}

1001. A + B Problem 1002. 几位数？ 1003. 计算 a 的 n 次方 1004. 值班 1005. SQUINT 1006. 求斜边 1007. 求 x 的 y 次方 1008. Sum of digit 1009. 工程 1010. 计算2的N次方 1011. 统计字符及行数 1012. 津津的书架 1013. 绝对值排序 1014. Sort it… 1015. 排序去重 1016. 键盘 1017. 成绩排序 1018. 询问队员身高 1019. 排序 1020. 文献排序 1021. 鞍点 1022. 数组排序 1023. 学生信息处理 1024. 单词表 1025. 商品推荐 1026. 成绩计算 1027. 发愁 1028. 指数比例 1029. 字串非重复字符数排序 1030. 素数个数排序 1031. HTTP与HTTPS 1032. 买书 1033. 自修室 1034. When I sort… 1035. 文件排序 1036. Search Web Pages 1037. 成绩排序 1038. 极坐标排序 1039. 道路排序 1040. 按整数最高位的值排序 1041. 闪卡销售 1042. Maya历日期的排序 1043. 字串排序 1044. 按数据中1的位数排序 1045. Hosts排序 1046. DNA 排序题 1047. 随机排序 1048. 行数据的排序 1049. 最小向量点积 1050. 字符排序 1051. 分数链表排序 1052. KL排序 1053. 邮件地址排序 1054. Holes 1055. Pinhole Imaging 1056. 重力加速度 1057. 链表整理 1058. 起床 1059. 火仙花数 1060. 查询 1061. 菱形 1062. 孤独数 1063. sunny的密码 1064. Hard to Believe, but True! 1065. Wavelet Compression 1066. 达到回文数 1067. 成绩统计 1068. 歌德巴赫猜想 1069. 买房子 1070. 魔方阵 1071. 数据密度 1072. 点名 1073. Familial Numbers 1074. 统计不同的最简真分数的个数 1075. 付钱 1076. 农场 1077. 3的倍数 1078. 数学手稿 1079. 判断 IP 1080. 卡片 1081. 替换 1082. ROT13加密和解密 1083. 计算n!右端0的个数(I) 1084. 天黑请闭眼 1085. 是坚挺数吗？ 1086. 单向链表中的节点删除 1087. 拥塞的城市 1088. 维吉尼亚密码 1089. 重复数 1090. N个整数中1的个数 1091. 小明生日 1092. GCD and LCM 1093. 完美数 1094. Soda Surpler 1095. 端午节快乐 1096. 加密1 1097. 最小公倍数 1098. 矩形个数 1099. Switching Lights 1100. 糖果 1101. 求三元组个数 1102. ZigZag 1103. 蛇行图案 1104. 数字猜想问题 1105. 巧克力 1106. 问候 1107. 坏掉的彩灯 1108. 闰年问题 1109. 计算内部回报率 1110. 最长的等差数列 1111. 找数 1112. 多次函数 1113. 波浪图 1114. 循环小数 1115. 圆和正方形 1116. 字符组合 1117. 连续正整数之和 1118. 4个值的和为0（Ⅱ） 1119. 纯虚数的幂 1120. 双阶乘的质因数个数 1121. 求和 1122. 移动游戏 1123. 位与数对个数 1124. 整数分组 1125. 分数的精确值 1126. 生理高峰 1127. 反转字符串 1128. 统计字符 1129. Welcome to 2009 ACM selective trial 1130. Capitalize 1131. 0 and 1 1132. 围栏 1133. 统计字母频率 1134. DongDong学英语 1135. Phone Number 1136. 分析字符 1137. 字母替换 1138. 删除子串 1139. 字符频率 1140. 单词出现次数 1141. A+B 1142. 字符串的幂 1143. 平衡三进制 1144. 字母替换 1145. 字符串重排 1146. 字符串替换 1147. 字符串消除 1148. All in All 1149. URL 1150. 统计单词个数 1151. 密码产生器 1152. 科学计数法 1153. 特殊加密 1154. 字串间距 1155. 数据压缩 1156. Base64编码 1157. n! 进制 1158. 搜索联系人 1159. 找数(II) 1160. 统计字符串个数 1161. 查找单词 1162. 排版 1163. 莫尔斯电码 1164. 解密字符串 1165. 完美度 1166. 分数的加减运算 1167. 字串变换 1168. GPS数据处理 1169. 电子邮件地址验证 1170. 大话西游 1171. 数字拆分 1172. 完全加括号的矩阵连乘积 1173. 0-1背包问题 1174. Fj & haozi 1175. 统计特定字串模式的个数 1176. 求上升子序列和的最大值 1177. 小型组合数 1178. 不重复正整数 1179. 单词的划分 1180. 计算多项式的系数 1181. 台阶走法数 1182. 整齐打印 (print neatly) 1183. 变换种类数 1184. 双调巡游 1185. 整数分解 1186. 路由结点 1187. 计算n!右端0的个数(II) 1188. 凹数 1189. 整数的质因子分解 1190. 质因数 1191. 因子平方和 1192. Prime 1193. 抽奖 1194. 素数进制A+B 1195. 互素勾股数 1196. 幂次转换 1197. IP Address 1198. 二进制位不同的个数 1199. 二进制与十六进制 1200. 非重复二进制串 1201. 进制转换 1202. 十六进制 1203. 2333进制 1204. 神秘信息 1205. 十六进制加法 1206. 进制数位和均值 1207. 负基数进制转换 1208. 方幂数列 1209. 内存显示 1210. 八进制小数 1211. 素进制链表 1212. 斐波那契数列 1213. 短信激活码 1214. Problem A+B (Big Integer) 1215. 计算a的n次方的大整数 1216. 十进制数列项 1217. 遥远距离 1218. 阶乘之和 1219. 高次方数的尾数 1220. 二进制倒置 1221. 最小不重复数 1222. sunny的烦恼 1223. 泰波拿契数列的前74项 1224. 母牛生小牛 1225. 求和 1226. 数列项 1227. 种田 1228. 计算数字之和 1229. 三元斐波纳奇数列 1230. 地铁站 1231. 四元一次方程 1232. 卡片游戏 1233. 查询Ⅱ 1234. 星巴克连锁店 1235. 波兰表达式 1236. 一元多项式乘法 1237. 链表运算 1238. 符号方程求解 1239. 小数转化分数 1240. 构造多项式 1241. 多项式分解 1242. 最近点对 1243. 集合运算 1244. 公共元素 1245. 零食 1246. 矩阵相加 1247. Light 1248. 华师大卫星照片 1249. 次大黑区域 1250. 小强的生日 1251. 小巴菲特买股票 1252. 小香浓范诺编码 1253. 构造字典序最小字符串 1254. 一个游戏 1255. 链表查询 1256. 数螃蟹 1257. 数青蛙 1258. 数蝌蚪 1259. 恢复单词 1260. 数位和 1261. 谁是第一名 1262. 记忆碎片 1263. 徒弟的下山之路

程序设计能力实训

输入格式

输出格式

样例

提示

题目列表

服务

开源

关于我们